Question

A 2.0 µC particle with a kinetic energy of 0.10 J enters a uniform magnetic field of magnitude 0.10 T. In the field, the particle moves in a circular path of a radius 3.0 m. Find the mass of the particle.3.7 x 10-12 kg3.1 x 10-12 kg4.2 x 10-12 kg1.3 x 10-12 kg1.8 x 10-12 kg

Answer 1

To calculate the mass of the particle, we can use the formulas for centripetal force and the magnetic force. By setting these forces equal to each other and solving for the mass, we find that it is approximately 3.7 x 10^-12 kg.

Step-by-step explanation:

To find the mass of the particle, we can use the formula for centripetal force. The centripetal force is provided by the magnetic force in this case. The magnetic force can be calculated using the formula F = qvB, where q is the charge of the particle, v is its velocity, and B is the magnetic field strength.

Since we know the charge of the particle (2.0 µC), the velocity (which can be calculated from the kinetic energy using the formula KE = 0.5mv^2), and the magnetic field strength (0.10 T), we can plug these values into the formula to calculate the magnetic force. Then, we can set this force equal to the centripetal force, which is given by F = mv^2/r, where m is the mass of the particle and r is the radius of the circular path.

After simplifying the equations, we can solve for the mass of the particle and find that it is approximately 3.7 x 10^-12 kg.

Answer 2

Given:

The charge of the particle, q=2.0 μC

The kinetic energy of the particle, K=0.10 J

The magnetic field, B=0.10 T

The radius of the path of the particle, r=3.0 m

To find:

The mass of the particle.

Step-by-step explanation:

The magnetic force acting on the particle is providing the particle with the necessary centripetal force.

Therefore the centripetal force acting on the particle is equal to the magnetic force acting on it.

Thus,

`(mv^2)/(r)=\text{qvB}`

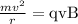
Where m is the mass of the particle and v is its velocity.

On simplifying the above equation,

`\begin{gathered} (mv)/(r)=qB \\ \Rightarrow v=(qrB)/(m) \end{gathered}`

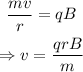
The kinetic energy of the particle is given by,

`K=(1)/(2)mv^2`

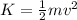
On substituting the value of v in the above equation,

`\begin{gathered} K=(1)/(2)m*((qrB)/(m))^2 \\ \Rightarrow K=(1)/(2m)(qrB)^2 \\ \Rightarrow m=(1)/(2K)(qrB)^2_{} \end{gathered}`

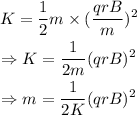
On substituting the known values in the above equation,

`\begin{gathered} m=(1)/(2*0.10)*(2.0*10^(-6)*3.0*0.10)^2 \\ =1.8*10^(-12)\text{ kg} \end{gathered}`

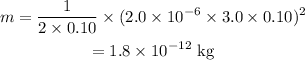
Final answer:

The mass of the particle is 1.8×10⁻¹² kg