Question

Instructions: Select the correct answer from each drop-down menu.

Graph the function y = f(x) = x2.
If the graph of the given function were shifted six units to the left, the new graph would represent the function,
A.) y=f(x+6) =(x+6)^2
B.) y=f(x-6)=(x-6)^2
C.) y=f(x)+6=x^2+6
D.) y=f(x)-6=x^2-6
If the graph of the given function were shifted upward by six units, the new graph would represent the function,
A.) y=f(x+6)=(x+6)^2
B.) y=f(x-6)=(x-6)^2
C.) y=f(x)+6=x^2+6
D.) y=f(x)-6=x^2-6
For the same y-values, the corresponding x-values of the function,
A.) y=f(3x/2)=(3x/2)^2
B.) y=f(2x/3)=(2x/3)^2
C.) y=f(x+1.5)=(x+1.5)^2
D.) y=f(x)+1.5=x^2+1.5
are 1.5 times of the x-values of the function y = f(x) = x2.

Answer 1

The answers are A, C, A in the order they are listed

Answer 2

1) Option A

2) Option C

3) Option A

Explanation:

We have given that : function
`y=f(x)=x^2`

1) If the graph of the given function were shifted six units to the left

translation to left means b unit is add on the function

i.e f(x)=f(x+b)

Therefore,the new graph have the function
`y=f(x+6)=(x+6)^2`

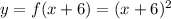
so, Option A is correct

2) If the graph of the given function were shifted upward by six units

translation to upward means b unit is add to the function

i.e f(x)=f(x)+b

Therefore,the new graph have the function
`y=f(x)+6=x^2+6`

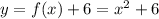
so, Option C is correct

3) 1.5 times of the x-values of the function
`y=f(x)=x^2`

1.5 times of the x-values means 1.5x = 3x/2

Therefore,
`y=f(3x/2)=(3x/2)^2`

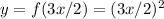
So, Option A is correct