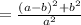Question

What is the ratio of the area of the inner square to the area of the outer square?

A: (a-b)2=b2/a2

B: a2-b2/a2

C: (a-b)2/(a+b)2

D: (ab)2/(a+b)2

Answer 1

I got this fraction:

frac{(a-b)^2+b^2}{a^2}

(I got the answer correct)

Hope this is helpful :)

Explanation:

Answer 2

`((a-b)^2+b^2)/(a^2)`

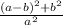
Explanation:

Since, By the given diagram,

The side of the inner square = Distance between the points (0,b) and (a-b,0)

`=√((a-b-0)^2+(0-b)^2)`

`=√((a-b)^2+b^2)`

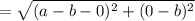
Thus the area of the inner square = (side)²

`=(√((a-b)^2+b^2))^2`

`=(a-b)^2+b^2\text{ square cm}`

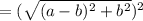
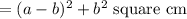
Now, the side of the outer square = Distance between the points (0,0) and (a,0),

`=√((a-0)^2+0^2)`

`=√(a^2)=a`

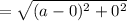
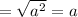
Thus, the area of the outer square = (side)²

`=a^2\text{ square cm}`

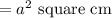
Hence, the ratio of the area of the inner square to the area of the outer square

`=((a-b)^2+b^2)/(a^2)`