Question

What is the general form of the equation of a circle with center at (a, b) and radius of length m?

A: x2 + y2 − 2ax − 2by + (a2 + b2 − m2) = 0

B: x2 + y2 + 2ax + 2by + (a2 + b2 − m2) = 0

C: x2 + y2 − 2ax − 2by + (a + b − m2) = 0

D: x2 + y2 + 2ax + 2by + a2 + b2 = -m2

Answer 1

the equation of a circle with center (h,k) and radius r is

`(x-h)^2+(y-k)^2=r^2`

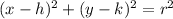
convert it to that form by comleting the square for the x and y terms
or, we can just expand what we know

expand
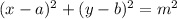
`(x-a)^2+(y-b)^2=m^2` and make it equal to 0
so expanding we get

`x^2-2ax+a^2+y^2-2by+b^2=m^2`
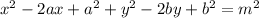
minus m^2 from both sides

`x^2-2ax+a^2+y^2-2by+b^2-m^2=0`
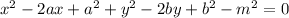
arranging in decreasing power order with m² at the end

`x^2+y^2-2ax+-2by+a^2+b^2-m^2=0`
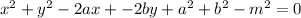
that is option A


answer is A