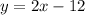Question

Find the slope-intercept form of the line that passes through the point (3, -6) and is parallel tothe line 4x-2y = -3.

Answer 1

The slope-intercept form is an equation in the form y = mx + b, where m is the slope and b the intercept with the y-axis.

We have the line 4x-2y = -3, let's arrange it into the slope-intercept form:

`\begin{gathered} 4x-2y=-3 \\ -2y=-4x-3 \\ y=2x+(3)/(2) \end{gathered}`

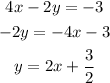
When two lines are parallel, they have the same slope, in the above equation, the slope is 2.

We plug in m=2 in the equation, to have an equation in the form of y = 2x+b, we need to find the value of b (intercept with the y-axis).

To find b, we plug in the point that passes through the line (3,-6)

`\begin{gathered} y=2x+b \\ -6=2\cdot3+b \\ b=-6-6=-12 \end{gathered}`

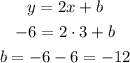
Now we plug in m = 2 and b = -12, in the slope-intercept form, to get the equation of the line that passes through the point (3,-6) and is parallel to line 4x-2y=-3:

`y=2x-12`