Question

How do I solve this and what is the answer

Answer 1

The unit circle is a circle with a radius of 1. Because of this, the coordinates of any point at this circle will correspond to (cosΘ, sinΘ). Where Θ is the given angle.

In this case, you have Θ=π/4

Then you need to find the values for sin(π/4) and cos(π/4) to find the point

First, let's convert π/4 into degrees

`(\pi)/(4)\text{rad }\cdot\text{ }\frac{180\circ}{\pi\text{ rad}}=(180)/(4)=45\circ^{}`

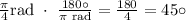
Now imagine a right triangle with one of the acute angles set to 45°, the internal angles of a right triangle have to sum 180°, then if you have a 90° and a 45° angle, then the other one will be 180°-90°-45°=45°. Then you will have an isosceles triangle.

By setting the length of one of the sides adjacent to the right angle to

1 and applying the Pythagorean theorem, you'll find the length of the hypotenuse as follows:

`\begin{gathered} a^2+b^2=h^2 \\ 1^2+1^2=h^2 \\ h=\sqrt[]{1^2+1^2}=\sqrt[]{2} \end{gathered}`

Then the cosine is given by:

`\begin{gathered} \cos (45)=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{1}{\sqrt[]{2}}\text{ multiply the numerator and denominator by }\sqrt[\square]{2} \\ \cos (45)=\frac{1\cdot\sqrt[]{2}}{\sqrt[]{2}\cdot\sqrt[]{2}}=\frac{\sqrt[]{2}}{2} \end{gathered}`

Now you can find the sine by:

`\begin{gathered} \sin (45)=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{1}{\sqrt[]{2}}\text{ multiply the numerator and denominator by }\sqrt[\square]{2} \\ \sin (45)=\frac{1\cdot\sqrt[]{2}}{\sqrt[]{2}\cdot\sqrt[]{2}}=\frac{\sqrt[]{2}}{2} \end{gathered}`

Then the coordinates of the point will be (cos45, sin45) = (√2/2, √2/2)