Question

Candy draws a square design with a side length of x inches for the window at the pet shop. She takes the design to the printer and asks for a sign that has an area of 16x2 – 40x + 25 square inches. What is the side length, in inches, of the pet shop sign?

Answer 1

B

Explanation:

Answer 2

The length of the sign is
`(4x-5)` inches

Explanation:

We are given that,

Area of the square design =
`16x^2-40x+25`

We will first find the roots of the equation
`16x^2-40x+2=0`

The roots of the quadratic equation
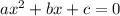`ax^2+bx+c=0` are given by
`x=(-b\pm√(b^2-4ac))/(2a)`

On comparing, a= 16, b= -40 and c= 25

So, the roots of the equation are,

`x=(40\pm√((-40)^2-4* 16* 25))/(2* 16)`

i.e.
`x=(40\pm√(1600-1600))/(32)`

i.e.
`x=(40\pm√(0))/(32)`

i.e.
`x=(40)/(32)`

i.e.
`x=(5)/(4)`

That is, the factors of the polynomial
`16x^2-40x+25` are
`(4x-5)` and
`4x-5`.

So, Area of the square design =
`16x^2-40x+25` =
`(4x-5)^2`

Since, Area of a square =
`Length^2`

Thus, the length of the sign is
`(4x-5)` inches