Question

Is x − 8 a factor of the function f(x) = −2x3 + 17x2 − 64? Explain.

Answer 1

To determine if x - 8 is a factor of the function
`f(x) = -2x^3 + 17x^2 - 64,` we need to check if f(8) = 0.

Step-by-step explanation:

To determine if x - 8 is a factor of the function
`f(x) = -2x^3 + 17x^2 - 64`, we need to check if f(8) = 0. If f(8) = 0, then x - 8 is a factor.

Let's substitute x = 8 into the function:

`f(8) = -2(8)^3 + 17(8)^2 - 64`

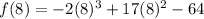
f(8) = -2(512) + 17(64) - 64

f(8) = -1024 + 1088 - 64

f(8) = 0

Since f(8) = 0, x - 8 is a factor of the function.

Answer 2

Answer: The answer is YES.

Step-by-step explanation: We are given to check whether (x - 8) is a factor of the function
`f(x)=-2x^3+17x^2-64.`

Factor Theorem states that if (x - a) is a factor of P(x), the we must have P(a) = 0.

We have

`f(8)\\\\=-2* 8^3+17* 8^2-64\\\\=-2* 512+17* 64-64\\\\=-2048+16* 64\\\\=-1024+1024\\\\=0.`

Thus, (x - 8) is a factor of f(x).