Question

1. Consider a student loan of ​$17,500 at a fixed APR of 12​% for 20 years. What is the monthly payment?

2. Consider a student loan of ​$25,000 at a fixed APR of 6​% for 15 years. What is the monthly payment?

3. Consider a home mortgage of ​$225,000 at a fixed APR of 4.5​% for 20 years. What is the monthly payment?

4. Consider a home mortgage of ​$225,000 at a fixed APR of 6​% for 30 years. What is the monthly payment?

5. Suppose that on January 1 you have a balance of ​$3000 on a credit card whose APR is 21​%, which you want to pay off in 1 year. Assume that you make no additional charges to the card after January 1. Calculate monthly payment

6. Suppose that on January 1 you have a balance of ​$4500 on a credit card whose APR is 17​%, which you want to pay off in 3 years. Assume that you make no additional charges to the card after January 1. Calculate monthly payment

Answer 1

a) p = Pr/[1-(1+i)^-n]
Assuming the interest compounds monthly
p = 175000(.01)/[1 - 1/(1.01)^240] = $1926.90

b) 240*1926.90 = $462,456

c) 175000/462456 = 37.84% is paid to principal and 100-37.84 = 62.16% is paid to interest.

Answer 2

The EMI formula is :

`EMI=(p* r*(1+r)^(n))/((1+r)^(n)-1)`

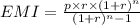
Part 1.

p = 17500

r =
`12/12/100=0.01`

n =
`12*20=240`

Putting values in formula we get

`(17500*0.01*(1+0.01)^(240))/((1+0.01)^(240)-1)`

=>
`(17500*0.01*(1.01)^(240))/((1.01)^(240)-1)`

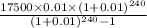
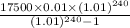
= $192.69

Part 2.

p = 25000

r =
`6/12/100=0.005`

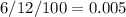
n =
`12*15=180`

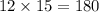
Putting values in formula we get

`(25000*0.005*(1+0.005)^(180))/((1+0.005)^(180)-1)`

=>
`(25000*0.005*(1.005)^(180))/((1.005)^(180)-1)`

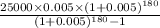
= $210.96

Part 3.

p = 225000

r =
`4.5/12/100=0.00375`

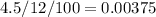
n =
`12*20=240`

Putting values in formula we get

`(225000*0.00375*(1+0.00375)^(240))/((1+0.00375)^(240)-1)`

=>
`(225000*0.00375*(1.00375)^(240))/((1.00375)^(240)-1)`

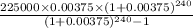
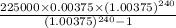
= $1423.46

Part 4.

p = 225000

r =
`6/12/100=0.005`

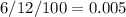
n =
`12*30=360`

Putting values in formula we get

`(225000*0.005*(1+0.005)^(360))/((1+0.005)^(360)-1)`

=>
`(225000*0.005*(1.005)^(360))/((1.005)^(360)-1)`

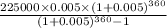
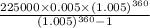
= $1348.98

Part 5.

p = 3000

r =
`21/12/100=0.0175`

n = 12

Putting values in formula we get

`(3000*0.0175*(1+0.0175)^(12))/((1+0.0175)^(12)-1)`

=>
`(3000*0.0175*(1.0175)^(12))/((1.0175)^(12)-1)`

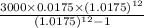
= $279.35

Part 6.

p = 4500

r =
`17/12/100=0.014166`

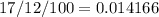
n =
`12*3=36`

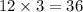
Putting values in formula we get

`(4500*0.014166*(1+0.014166)^(36))/((1+0.014166)^(36)-1)`

=>
`(4500*0.014166*(1.014166)^(36))/((1.014166)^(36)-1)`

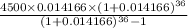
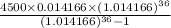
= $160.43