1 Answer

Luis Lobo · Answer 1 · 2022-10-20T16:52:20+0000

Answer:

$\boxed {\boxed {\sf About \ 5 \ centimeters }}$

Explanation:

The area of a circle is found using this formula:

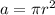
$a= \pi r^2$

We know the area of the disc is 78.53 square centimeters and 3.14 is being used for pi.

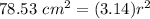
$78.53 \ cm^2 = (3.14) r^2$

We are solving for the radius, so we must isolate the variable r.

3.14 and r² are being multiplied. The inverse of multiplication is division, so divide both sides by 3.14

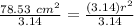
$(78.53 \ cm^2)/(3.14) = ((3.14) r^2)/(3.14)$

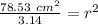
$(78.53 \ cm^2)/(3.14) =r^2$

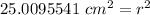
$25.0095541 \ cm^2 = r^2$

r is being squared, so we must take the square root of both sides.

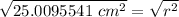
$√(25.0095541 \ cm^2) = \sqrt {r^2}$

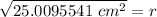
$√(25.0095541 \ cm^2) = r$

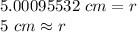
$5.00095532 \ cm = r \\5 \ cm \approx r$

The radius of the disc is about 5 centimeters.

Please log in or register to add a comment.