Question

Two asteroids are 50,000 m apart. one has a mass of 5 x 10^8 kg. If the force of gravity between them is 8.67 x 10 ^ -2 N, what is the mass of the other asteroid?

Answer 1

6.5 *10^9 kg
is the mass of the second one

Answer 2

The mass of the other asteroid is
`m_2=6.49* 10^9\ kg`.

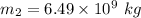Step-by-step explanation:

Given that,

Mass of one asteroid,
`m=5* 10^8\ kg`

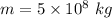
The separation between two asteroids, r = 50,000 m

The force of gravity between asteroids,
`F=8.67* 10^(-2)\ N`

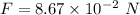
We need to find the mass of the other asteroid. The gravitational force acting between two masses is given by :

`F=G(m_1m_2)/(r^2)`

`m_2` is the mass of other asteroid

`m_2=(Fr^2)/(Gm_1)`

`m_2=(8.67* 10^(-2)* (50000)^2)/(6.67* 10^(-11)* 5* 10^8)`

`m_2=6.49* 10^9\ kg`

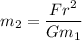
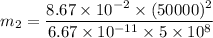
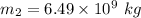
So, the mass of the other asteroid is
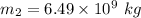`m_2=6.49* 10^9\ kg`. Hence, this is the required solution.