Question

F(x) = -x^2-12 find f(-3)

Answer 1

`\boxed {\boxed {\sf f(-3)= -21}}`

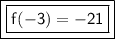
Explanation:

We are given the function:

`f(x)= -x^2-12`

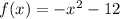
We want to find f(-3), so we must substitute -3 in for x.

`f(-3)= -(-3)^2 -12`

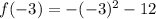
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Addition, Subtraction.

Solve the exponent.

• (-3)²= -3*-3 = 9

`f(-3)= -(9)-12`

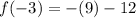
Distribute the -1 in.

`f(-3)= -9-12`

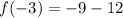
Subtract.

`f(-3)= -21`

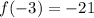
For the function -x²-12, f(-3) is equal to 21

Answer 2

-1 * (-3)^2 - 12 = -1 * 9 -12 = -9 - 12 = -21

Explanation: