Question

Select all the expressions that equal 6-1 D 6-5.62 () -16% D 6.63

Answer 1

The given expression is;

`6^(-10)`

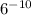
A)

`6^(-5)\cdot6^2_{}`

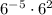
Since bases of both the terms are same i.e., 6

So, when multiplying two powers that have the same base, you can add the exponents.

`\begin{gathered} 6^(-5)\cdot6^2_{}=6^(-5+2) \\ 6^(-5)\cdot6^2_{}=6^(-3) \\ \text{Since, 6}^(-3)\\e6^(-10) \end{gathered}`

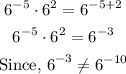
So, Option A is not the right answer;

B)

`((1)/(6^2))^5`

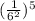
Apply the power rule of exponents;

`\begin{gathered} ((1)/(6^2))^5=(6^(-2))^5^{} \\ ((1)/(6^2))^5=6^(-10) \\ \text{ Since, the given expression is 6}^(-10) \\ So,6^(-10)=6^(-10) \end{gathered}`

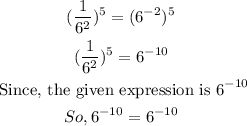
Thus, Option B is the right answer

C)

`(6^(-5))^2`

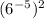
Apply the exponents rule;

`\begin{gathered} (6^(-5))^2=6^(-10) \\ \text{ Since, the given expression is; 6}^(-10) \\ 6^(-10)=6^(-10) \end{gathered}`

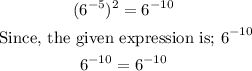
Therefore, Option C is the right answer

D)

`(6^5\cdot6^(-3))/(6^(-8))`

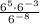
Simplify the expression;

since the bases are same so the in the multiplication the exponent value will be add up and during division, the exponent value will be subtract;

`\begin{gathered} (6^5\cdot6^(-3))/(6^(-8))=(6^2)/(6^(-8)) \\ (6^5\cdot6^(-3))/(6^(-8))=6^(2-(-8)) \\ (6^5\cdot6^(-3))/(6^(-8))=6^(2+8) \\ (6^5\cdot6^(-3))/(6^(-8))=6^(10) \\ \text{ Since, the given expression is 6}^(-10) \\ and6^(-10)\\e6^(10) \end{gathered}`

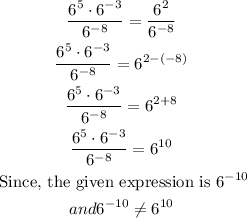
Therefore, Option D is not the right answer

E)

`(6^(-3))/(6^7)`

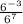
Simplify the expression by using division rule of exponent;

To divide exponents (or powers) with the same base, subtract the exponents:

`\begin{gathered} (6^(-3))/(6^7)=6^(-3-7) \\ (6^(-3))/(6^7)=6^(-10) \\ \text{ Since, the given expression is 6}^(-10) \\ 6^(-10)=6^(-10) \end{gathered}`

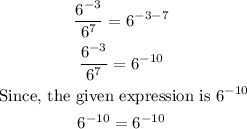
So, option E is the correct answer

Answer : B, C,