Answer:
1)

2) option A
3) option B
Explanation:
1) Given: The ordered pairs model an exponential function, where j is the function name and e is the input variable.
{(1, 10), (2, 50), (3, 250), (4, 1250)}
Let an exponential function

Now, put (1,10) ⇒10=ab .....(1)
put (2,50) ⇒
 ....(2)
....(2)
divide (1) and (2)
we get b=5 then put back in (1)
we get 10=a(5)⇒ a=10/5= 2
therefore the required function is

For j is the function name and e is the input variable
the function is

2) Given: The population of a pack of wolves is 88. The population is expected to grow at a rate of 2.5% each year.
To find: What function equation represents the population of the pack of wolves after t years
solution :
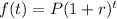
where P-population , r- growth rate , t -time
putting value we get,
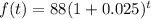
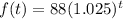
therefore, option A is correct
3) Given: Ramon bought a bicycle for $478. The value of the bicycle is expected to decrease at a rate of 6.5% each year.
To find: What function equation represents the value of the bicycle after t years.
solution :

where P-population , r- decay rate , t -time
putting values we get,
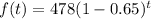
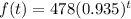
therefore, option B is correct