Question

Triangle ABC is inscribed in the circle below. Using the measurements provided in the diagram, find the measure of arc AB.

Answer 1

Given: A triangle ABC inscribed in a circle as shown in the shown image in the question

To Determine: The measure of the arc AB

Solution

Re-draw the diagram

Let the center of the circle be O as shown in the image above

It can be seen that the angle subtended by the arc BC is the same as angle BOC

Using the circle theorem, the angle at the center is twice angle at the circumference.

The angle subtended at the circumference by the arc BC is angle BAC

Therefore

`\angle BOC=2*\angle BAC`
`\begin{gathered} \angle BOC=112^2 \\ Therefore \\ 2*\angle BAC=112^0 \\ \angle BAC=(112^0)/(2) \\ \angle BAC=56^0 \end{gathered}`

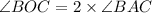
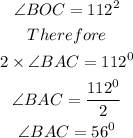
Note: The angle A, angle B and angle C formed the interior angles of the triangle ABC. Therefore

`\begin{gathered} \angle A+\angle B+\angle C=180^0 \\ 56^0+65^0+\angle C^0=180^0 \\ 121^0+\angle C=180^0 \\ \angle C=180^0-121^0 \\ \angle C=59^0 \end{gathered}`

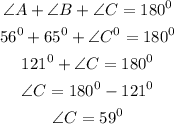
It can be observed that angle C is the angle subtended by arc AB at the circumference and angle AOB is the angle subtended by the arc AB at the center. Using the circle theorem that angle subtended at the center is twice angle subtended at the circumference

Therefore

`\begin{gathered} \angle AOB=2*\angle C \\ \angle AOB=2*59^0 \\ \angle AOB=118^0 \end{gathered}`

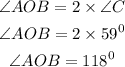
Hence, the measure of arc AB is 118⁰