From the information provided, we know that Mr Chandler travels at a speed of 40 miles per hour (40mph). He also left 5 hours before Mrs Chandler.
Therefore, we can tell that for 5 hours he has travelled
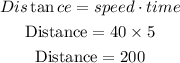
We shall now label the total distance covered as d, and the number of hours taken (time) as t.
We now have for Mr Chandler;
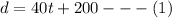
For Mrs Chandler, we would have;

We would now solve the system of equations as follows;

This result shows that, travelling at the speed given for both Mr and Mrs Chandler, it would take her 5 hours to catch up with him.
ANSWER:
5 hours
PART B
If Mr Reeds leaves 3.5 hours ahead of Mrs Reeds and he travels at the speed of 55 miles per hour (55 mph), then his distance would be;
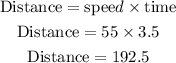
If the total distance covered is given as d, then for Mr Reeds the total distance would be;
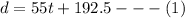
For Mrs Reeds, we would have;

Note that d represents the total distance covered and t represents the time taken (in hours).
We shall now solve the system of equations, as follows;
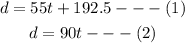
We shall substitute for the value of d into equation two. Note that d = d, which means equation (1) equals equation (2). We now have;
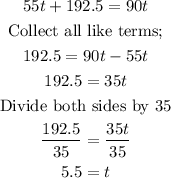
The calculations here shows that travelling at the speeds given for both of them, it would take Mrs Reeds 5.5 hours to catch up with Mr Reeds.
ANSWER:
5.5 hours