Question

Pine Bluff Middle School is having its annual Spring Fling dance, which will cost $400. The student treasurer reported that the dance fund has $75 left over from last year. Each ticket to the dance costs $4.

Let t represent the number of tickets sold. Write an inequality to determine how many tickets must be sold to pay for this year's dance.

Answer 1

The required inequality is 4t + 75 ≥ 400

4t ≥ 400 - 75
4t ≥ 325
t ≥ 81.25

Therefore, 82 tickets must be sold to pay for this year's dance

Answer 2

The inequality required is:
`75 + 4t \geq 400`

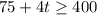
and 82 tickets must be sold to pay for this year's dance.

Explanation:

Let t represents the number of tickets sold.

Given: Each ticket to the dance costs is $ 4 and the student treasure reported that the dance fund has $ 75 left over from last year.

Since, each ticket to the dance sold is $4,

therefore the total cost to the dance is 4t

Together with the $75 left carry over,

then we have; 75 + 4t

As per the given conditions :

They must make at least $400 to pay for the dance i.e it must be more than or equal to 400;

which gives you the inequality:
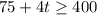`75 + 4t \geq 400` where t is the number of tickets sold.

Now, solve this inequality which gives you how many tickets must be sold to pay for this year's dance.

`75 + 4t \geq 400`

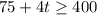
Subtraction property of equality states that you subtract the same number to both sides of an equation.

Subtract 75 to both sides of an equation;

`75 + 4t -75 \geq 400-75`

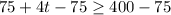
Simplify:

`4t\geq 325`

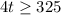
Division property of equality states that you divide the same number to both sides of an equation.

divide by 4 to both sides of an equation;

`(4t)/(4) \geq (325)/(4)`

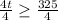
Simplify:

`t\geq 81.25`

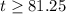
Since, you cannot sell quarter of ticket ;

so, 81.25 rounded up to 82

therefore, 82 tickets must be sold to pay for this year's dance.