Question

Solve the system of equations: 3x + 4y = 33 y = 2 - 4 11 Fill in the coordinates of the ordered pair:(

Answer 1

The system of equations we have is:

`\begin{gathered} \\ \mleft\{\begin{aligned}3x+4y=33 \\ y=x-4\end{aligned}\mright. \end{gathered}`

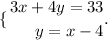
To solve it, we need to have the variables of both equations on the same side.

Step 1: Substract x from both sides of the second equation

`\begin{gathered} y-x=x-x-4 \\ y-x=-4 \\ -x+y=-4 \end{gathered}`

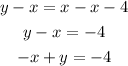
And now the system is:

`\{\begin{aligned}3x+4y=33 \\ -x+y=-4\end{aligned}`

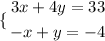
Step 2: We need to eliminate one variable to solve, for this reason now we multiply the second equation by 3

`\begin{gathered} 3(-x+y=-4) \\ -3x+3y=-12 \end{gathered}`

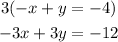
And we add this with the first equation of the system

`\begin{gathered} 3x+4y=33 \\ -3x+3y=-12 \\ ----------- \\ 0x+7y=21 \end{gathered}`

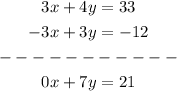
which is the same as:

`7y=21`

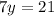
Step 3: solve this previous equation for y, by dividing both sides by 7

`\begin{gathered} (7y)/(7)=(21)/(7) \\ y=3 \end{gathered}`

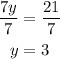
Step 4: with the value for y, we find the value of x.

Substituting y=3 in the second equation of the original system of equations:

`y=x-4`
`3=x-4`

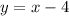
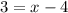
We add 4 to both sides:

`\begin{gathered} 3+4=x \\ 7=x \end{gathered}`

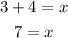
Answer: y=3 and x=7, representing the result as an ordered pair: (7, 3)