The system of equations we have is:
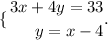
To solve it, we need to have the variables of both equations on the same side.
Step 1: Substract x from both sides of the second equation
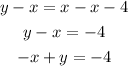
And now the system is:
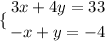
Step 2: We need to eliminate one variable to solve, for this reason now we multiply the second equation by 3
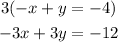
And we add this with the first equation of the system
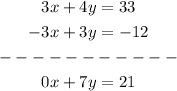
which is the same as:
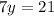
Step 3: solve this previous equation for y, by dividing both sides by 7
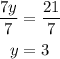
Step 4: with the value for y, we find the value of x.
Substituting y=3 in the second equation of the original system of equations:

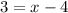
We add 4 to both sides:
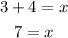
Answer: y=3 and x=7, representing the result as an ordered pair: (7, 3)