Question

Use the discriminant to determine the number of real-number solutions for the equation:

8x2 + 8x + 2 = 0
A. one solution
B. two solutions
C. no solutions
D. infinitely many solutions

Answer 1

I hope this helps you

Answer 2

A. One solution

Explanation:

Given quadratic equation is,

`8x^2+8x+2=0`

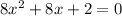
Since, if for a quadratic equation
`ax^2+bx+c`,

The discriminant,

`D=b^2-4ac > 0`

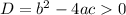
The equation has two real different solutions,

If D = 0,

The equation has one real solution with multiplicity two,

While, if D < 0,

The equation has two imaginary solutions,

Here, the discriminant,

`D=(8)^2-4* 8* 2=64-64 = 0`

Thus, by the above explanation,

It is clear that the given equation has one real solution,

Option A is correct.