Answer:
The correct option is 2.
Explanation:
Zina spends 1.5 hours setting up her sewing machine and making one hat.
The total amount of time spent making hats can be represented by the sequence
1.5, 2.25, 3.0, 3.75, ...
It is an AP, where first term is 1.5 and common difference is

The recursive formula of an AP is
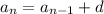
It can also be written as
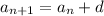
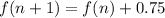
Therefore the correct option is 2.