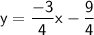Answer:
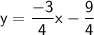
Explanation:
Equation of line: y = mx + b
Here m is the slope and b is the y-intercept.
First, let us find the slope of given line.
(-4 ,4) & (4 , -2)

![\sf = (-2-4)/(4-[-4])\\\\\\=(-6)/(4+4)\\\\\\=(-6)/(8)\\\\\\=(-3)/(4)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/5k93u3ha2c88f3k92lgb.png)
Parallel lines have same slope.
m = -3/4
Equation of the line:
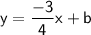
At x_intercept, y is 0. (-3 , 0). The line passes through the point (-3 ,0).
Substitute in the above equation and we can find the value of 'b'.
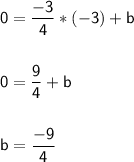
Equation of the required line: