Question

Find the measure of angle y

Answer 1

34

Explanation:

I did the test

Answer 2

ISOSCELES TRIANGLE

An isosceles triangle is a triangle that has two sides of equal length. In this exercise, we see small lines on two of the sides. This means that those sides are equal.

‎ ‏‏‎

Equalize the expressions:

6x - 23 = 4x + 9

Add 23 to both sides of the equation:

6x - 23 + 23 = 4x + 9 + 23

‎ ‏‏‎‎ ‏‏‎‎ 6x = 4x + 32

Substract 4x from both sides:

6x - 4x = 4x - 4x + 32

‏‏‎‎ 2x = 32

Finally, divide both sides by 2:

`\mathsf{(2x)/(2) = (32)/(2)}`

`\large{\boxed{\mathsf{x = 16}}}`

‎ ‏‏‎

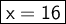
Now, let's find the measures of the angles:

• (6x - 23)° = 6(16) - 23 = 96 - 23 = 73°
• (4x + 9)° = 4(16) + 9 = 64 + 9 = 73°

‎ ‏‏‎

Remember: The sum of the three angles of any triangle is equal to 180 degrees. Let's find the measure of the angle Y:

73° + 73° + Y = 180°

146° + Y = 180°

Y = 180° - 146°

Y = 34°

‎ ‏‏‎

Answer. m∠Y = 34°

‎