Let
x---------> the length side of the rectangular area
y---------> the width side of the rectangular area
we know that
the area of the rectangle is equal to

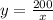 -----> equation
-----> equation

The perimeter of the rectangle is equal to

but remember that the fourth side of the rectangle will be formed by a portion of the barn wall
so
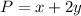 -----> equation
-----> equation
To minimize the cost we must minimize the perimeter
Substitute the equation
 in the equation
in the equation
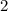
![P=x+2*[(200)/(x) ]](https://img.qammunity.org/2017/formulas/mathematics/high-school/u5japxzxujgpc4ubuf1995qn2oftpkx54c.png)
Using a graph tool
see the attached figure
The minimum of the graph is the point
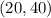
that means for
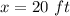
the perimeter is a minimum and equal to

Find the value of y
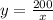
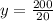

The cost of fencing is equal to
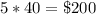
therefore
the answer is
the length side of the the fourth wall will be
