Given:
An exponential function goes through points (0, 14) and (4, 8750).
To find:
The function.
Solution:
The general form of an exponential function is
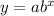 ...(i)
...(i)
It goes through points (0, 14) and (4, 8750). It means the the equation must be satisfied by these points.
Putting x=0 and y=14 in (i), we get
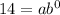
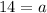
The value of a is 14.
Putting a=14, x=4 and y=8750 in (i), we get

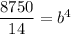
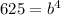
It can be written as
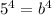

The value of b is 5.
Putting a=14 and b=5 in (i), we get

Therefore, the required exponential function is
 .
.