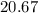Question

TRIGONOMETRY Find the area of the entertainment region round to two decimal places

Answer 1

Step-by-step explanation

In the first case, we will find the area of the triangle. This is given as;

`\begin{gathered} \text{Area of}\triangle=ab\sin \theta \\ =5*5\sin 40^0 \\ =16.0697 \end{gathered}`

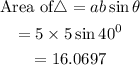
To get the area of the semicircle we will require the diameter of the semicircle, which is the unknown side of the triangle.

Let the unknown side be x

Therefore, we can use the cosine rule.

`\begin{gathered} x=\sqrt[]{a^2+b^2-2ab\cos \theta} \\ x=\sqrt[]{5^2+5^2-2*5*5\cos 40^0} \\ x=\sqrt[]{25^{}+25^{}-50\cos 40^0} \\ x=\sqrt[]{50^{}-50\cos 40^0} \\ x=3.4202 \end{gathered}`

x represents the diameter of the semicircle. We can then have the radius as half of x.

`r=(x)/(2)=(3.4202)/(2)=1.7101`

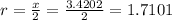
The area of the semicircle is given as

`\text{area of a semicircle =}(1)/(2)(\pi r^2)=(1)/(2)(\pi*1.7101*1.7101)=4.5937^{}`

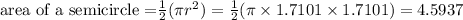
Therefore, the area of the shape is the sum of the triangle and the semi-circle.

`\begin{gathered} \text{Area of the shape =16.06}97+4.5937 \\ =20.67 \end{gathered}`

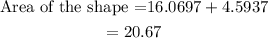
Answer:

`20.67`