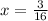Question

Solve the exponential equation 9^8x = 27

Answer 1

The answer is x=3/16

Answer 2

`x=(3)/(16)`

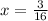
Explanation:

Given : Exponential function
`9^(8x)=27`

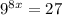
We have to solve the given exponential equation.

Consider the given exponential function
`9^(8x)=27`

`\mathrm{Convert\:}9^(8x)\mathrm{\:to\:base\:}3`

`9^(8x)=\left(3^2\right)^(8x)`

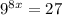
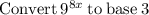
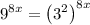
Function becomes,

`\left(3^2\right)^(8x)=27`

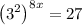
Convert 27 to base 3, we have,

`\left(3^2\right)^(8x)=3^3`

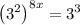
Apply exponent rule,
`\left(a^b\right)^c=a^(bc)`

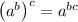
We have,
`3^(2\cdot \:8x)=3^3`

`\mathrm{If\:}a^(f\left(x\right))=a^(g\left(x\right))\mathrm{,\:then\:}f\left(x\right)=g\left(x\right)`

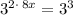
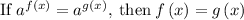
We have,

`2\cdot \:8x=3`

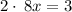
Simplify, we have,

`16x=3`

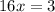
Thus,
`x=(3)/(16)`