Question

(8,-2)and(12,-6)1) put in slope intercept form2) solve the same points but in standard form

Answer 1

The slope intercept form​: y = -x + 6

In standard form, we have: x + y = 6

Step-by-step explanation:

1) The points: (8,-2)and(12,-6)

The slope intercept formula:

`y\text{ = mx +c}`

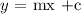
where m = slope and c = intercept

m = change in y/ change in x

`\begin{gathered} m\text{ = }((-6-(-2)))/((12-8)) \\ m\text{ = }(-6+2)/(4)\text{ = -4/4} \\ m\text{ = -1} \end{gathered}`

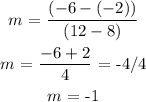
To get the intercept, insert the value of x and y using any of the points:

using point (8, -2) = (x, y)

y = -1x + c

-2 = -(8) + c

-2 = -8 + c

-2+8 = c

c = 6

y = -1(x) + 6

Equation of line with slope -1 and intercept 6

The slope intercept form​: y = -x + 6

2) In standard form: Ax + By = C

In our derived equation, A = -1, B = 1 and c = 6

y + x = 6

x + y = 6

In standard form, we have: x + y = 6