Question

The playing surfaces of two foosball tables are similar. The ratio of the corresponding sidelengths is 10:7. If the perimeter of the smaller is 42, what is the perimeter of the larger table?

Answer 1

Given:

Ratio of corresponding sides = 10 : 7

Perimeter of smaller table = 42

Total ratio = 10 + 7 = 17

Let's find the perimeter of the larger table.

Given that both tables are similar, it means the corresponding sides are proportional.

To find the ratio of the larger table, let's first find the total perimeter of the both tables:

`\frac{\text{smaller ratio}}{total\text{ ratio}}* T=perimeter\text{ of smaller table}`

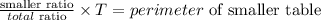
Where T represents the total ratio.

Thus, we have:

`\begin{gathered} (7)/(17)* T=42 \\ \\ \text{Multiply both sides by 17:} \\ (7)/(17)*17* T=42*17 \\ \\ 7T=714 \end{gathered}`

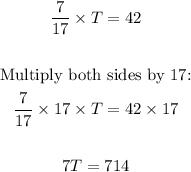
Divide both sides by 7:

`\begin{gathered} (7T)/(7)=(714)/(7) \\ \\ T=102 \end{gathered}`

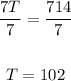
The total perimeter is 102.

To find the permeter of the larger table, we have:

Perimeter of larger table = Total perimeter - perimeter of smaller table.

Perimeter of larger table = 102 - 42

Perimeter of larger table = 60

Therefore, the perimeter of the larger table is 60.

ANSWER:

60