Question

80 POINTS!!!

A line segment has endpoints at (4, –6) and (0, 2). What is the slope of the given line segment? What is the midpoint of the given line segment? What is the slope of the perpendicular bisector of the given line segment? What is the equation, in slope-intercept form, of the perpendicular bisector?

Answer 1

Answer: the answers are in the explanation, they are also in order

Explanation:

-2

(2,-2)

1/2

y=(1/2)x - 3

Answer 2

1). Slope = (-2)

2). Midpoint = (2, -2)

3). Slope of the perpendicular bisector = (1/2)

4). Equation of perpendicular bisector will be x - 2y = 6

Explanation:

A line segment has the endpoints at (4, -6) and (0, 2).

1). Then the slope of the given line segment will be = (y - y')/(x - x') = (2 + 6)/(0 - 4) = 8/(-4) = (-2)

2). Mid point of the line segment is given by
`((x_(1)+x_(2))/(2)) , ((y_(1)+y_(2))/(2))`

Therefore midpoints of the line segment will be
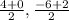`(4+0)/(2),(-6+2)/(2)` = (2, -2)

3). Slope of the perpendicular bisector is represented by
`m_(1).m_(2)=(-1)`

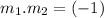
⇒ (-2)×m2 = (-1)

⇒
`m_(2)=(1)/(2)`

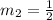
4). Now we have to find the equation of perpendicular bisector passing through (2, -2) and slope (1/2).

Since standard equation of the line will be given as y = mx + c

`y=(1)/(2)x+c` passes through (2, -2).

`(-2) = (1)/(2)(2) + c`

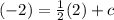
c = (-1) - 2 = -3

Finally the equation of perpendicular bisector will be

`y=(1)/(2)x+(-3)`

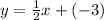
⇒ 2y = x - 6

⇒ 2y - x = -6

⇒ x - 2y = 6