Question

Which equation does the graph of the systems of equations solve? It's a quadratic graph opening down and quadratic graph opening up. They intersect at (0,3) and (2,-5).

(a)x2 - 2x + 3 = 2x2 - 8x - 3
(b)x2 - 2x + 3 = 2x2 - 8x + 3
(c)-x2 - 2x + 3 = 2x2 - 8x - 3
(d)-x2 - 2x + 3 = 2x2 - 8x + 3

Answer 1

(d)-x2 - 2x + 3 = 2x2 - 8x + 3

Explanation:

Answer 2

D.
`-x^(2) -2x+3=2x^(2) -8x+3`

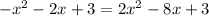
Explanation:

We are given that,

The graph of the system of equations is a 'quadratic graph opening down and a quadratic graph opening up'.

This means that one quadratic equation will have leading co-efficient positive and other will have leading co-efficient negative.

So, we get that options A and B are discarded.

Further it is provided that the graph intersect at ( 0,3 ) and ( 2,-5 ).

This means that the pair of points must satisfy the given system of equations.

So, according to the options:

C.
`-x^(2) -2x+3=2x^(2) -8x-3`

Putting x = 0, gives 3 = -3, which is not possible.

So, option C is dicarded.

D.
`-x^(2) -2x+3=2x^(2) -8x+3`

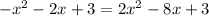
Putting x = 0 gives 3 = 3 and x = 2 gives -5 = -5.

Hence, the graph of the given system solves the equation
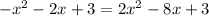`-x^(2) -2x+3=2x^(2) -8x+3`.