Question

A relation is plotted as a linear function on the coordinate plane starting at point C (0,−1) and ending at point D (2,−11) . What is the rate of change for the linear function and what is its initial value?

Answer 1

-1 - (-11) 10
---------- = ---
2 - 0 2

So your answer is 5 for the rate of change

Answer 2

The rate of change refers to the slope of the linear function, because the slope is actually a ration between the two variables. So, to find the slope, we use its definition:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

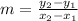
Now we replace the given points, being C the first point and D the second point:

`m=(-11-(-1))/(2-0)=(-11+1)/(2)=(-10)/(2)=-5`

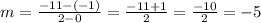
Therefore, the rate of change is -5, where the negative sign refers to a decreasing change, it's a decreasing linear function. In addition, the initial values is where the independent variable is zero, which is given in the point C (0;-1), so the initial condition is y = -1