Question

Factor 4n 4 + n 3. i need help fast 5

Answer 1

If you are simplifying only, the factored form is
`n^3(4n+1)`

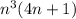
If you are factoring to solve, then the solutions are n = 0, multiplicity 3 and n =
`-(1)/(4)`

Explanation:

Factor out what is common between the 2 terms, which is n-cubed. Doing that gives you this:

`n^3(4n+1)`

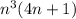
That is just simplified, not solved by factoring. It all depends upon what you are wanting to do with this. If you are solving it, we start from the simplified form and set each factor equal to 0 and solve for n:

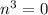`n^3=0` and 4n + 1 = 0

Because this is a 4th degree polynomial, we have 4 solutions. The first one is found in 4n + 1 = 0. Solving for n:

4n = -1 so

`n=-(1)/(4)`

That's one solution. The next 3 are found in

`n^3=0`

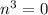
Undo that cubing by taking the cubed root of both sides:

`\sqrt[3]{n^3}=\sqrt[3]{0}`

The cubed root of n-cubed is just n; the cubed root of 0 is just 0, but we have 3 of them since we find only one root in 4n + 1.

So, again, if you are just simplifying, the answer is

`n^3(4n+1)`

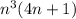
If you are solving, the solutions are

`n=-(1)/(4)` and n = 0, multiplicity 3