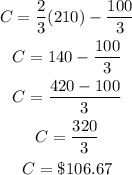Question

4. A contractor found that his labor cost for installing 80 feet of pipe was $20. He also found that his labor cost for installing 200 feet of pipe was $100. If the cost C in dollars is a linear function of the length L in feet, then what is the formula for this function? What would his labor cost be for installing 210 feet of pipe?

Answer 1

Since, the cost C in dollars is a linear function of the length L in feet, we can write:

`C=mL+b`

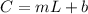
Where

m is the slope

b is the y-intercept of the line graphed.

The points are in the from (L, C) which is (length, cost). Given:

(80, 20) and (200, 100)

The slope (m) is:

`m=(y_2-y_1)/(x_2-x_1)`

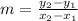
Let the points be:

`\begin{gathered} (x_1,y_1)=(80,20) \\ (x_2,y_2)=(200,100) \end{gathered}`

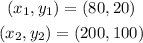
So slope is:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=\frac{100-20_{}}{200-80_{}} \\ m=(80)/(120) \\ m=(2)/(3) \end{gathered}`

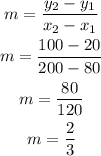
The equation becomes:

`C=(2)/(3)L+b`

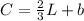
Let's take the point (L, C) = (80, 20) and find out b:

`\begin{gathered} C=(2)/(3)L+b \\ 20=(2)/(3)(80)+b \\ 20=(160)/(3)+b \\ b=20-(160)/(3) \\ b=(60-160)/(3) \\ b=(-100)/(3) \end{gathered}`

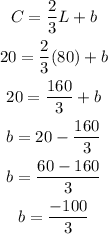
The formula for the function is:

`C=(2)/(3)L-(100)/(3)`

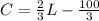
The cost of installing 210 feet of pipe:

We plug in L = 210 into formula and find C:

`\begin{gathered} C=(2)/(3)(210)-(100)/(3) \\ C=140-(100)/(3) \\ C=(420-100)/(3) \\ C=(320)/(3) \\ C=\$106.67 \end{gathered}`