The sample proportion is calculated as:
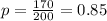
The critical value for significance level = 1 - 0.99 = 0.01, from the z table is z = 2.3263
Therefore, the 99%confidence interval is computed as follows:
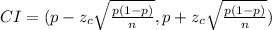
Where:
p = 0.85
zc = 2.3263
n = 200
Substitute the values we have:
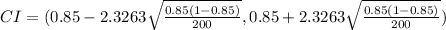
Simplify:
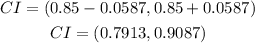
For 3 decimal places is (0.791, 0.909).
Answer: (0.791, 0.909)