Question

Out of 200 people sampled, 170 had kids. Based on this, construct a 99% confidence interval for the true population proportion of people with kids.Give your answers as decimals, to three places

Answer 1

The sample proportion is calculated as:

`p=(170)/(200)=0.85`

The critical value for significance level = 1 - 0.99 = 0.01, from the z table is z = 2.3263

Therefore, the 99%confidence interval is computed as follows:

`CI=(p-z_c\sqrt{(p(1-p))/(n)},p+z_c\sqrt{(p(1-p))/(n)})`

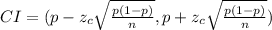
Where:

p = 0.85

zc = 2.3263

n = 200

Substitute the values we have:

`CI=(0.85-2.3263\sqrt{(0.85(1-0.85))/(200)},0.85+2.3263\sqrt{(0.85(1-0.85))/(200)})`

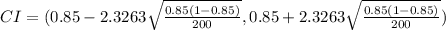
Simplify:

`\begin{gathered} CI=(0.85-0.0587,0.85+0.0587) \\ CI=(0.7913,0.9087) \end{gathered}`

For 3 decimal places is (0.791, 0.909).

Answer: (0.791, 0.909)