Question

Let θ be an angle in Quadrant II such that cot θ = -3. Find the exact values for sin θ, cos θ, and tan θ.

Answer 1

If angle theta is on Quadrant II, then it will have a coordinate of (-,+)


cot(theta) = x/y = -3/1
*Note: x^2 + y^2 = r^2 so, (-3^2) + (1^2) = [sqrt(10)]^2
r = sqrt(10)
sin(theta) = y/r = 1/sqrt(10)
cos(theta) = x/r = -3/sqrt (10)
tan(theta) = y/x = 1/-3

Answer 2

Here, I've attached a picture of the triangle that accompanies this explanation.

cot =
`(1)/(tan)` =
`(1)/( (sin)/(cos) )` =
`(cos)/(sin)`

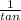
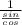
Now view the triangle.
PS. Angle theta will have a coordinate of (-, +) because it is in quadrant II.

sin of the angle would be opposite/hypotenuse, so sin =
`(1)/( √(10) )`
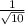cos of the angle would be adjacent/hypotenuse, so cos =
`(-3)/( √(10) )`
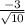tan of the angle would be opposite/adjacent, so tan =
`- (1)/(3)`