Question

An acute triangle has sides that are 14mm and 97mm long, respectively. The 3rd side of the triangle must be greater than what whole number of millimeters.

Answer 1

no because the greater is 97mm is a great difference between 14 and 97 so the answer is NO

Answer 2

Answer: The length of the third side is greater than 83 mm.

Step-by-step explanation: Given that an acute triangle has sides that are 14 mm and 97 mm long respectively.

We are to find the whole number of millimeters by which the length of he third side is greater.

Let x mm be the length of the length of the third side of the triangle.

Since the sum of the lengths of any two sides of a triangle is always greater than the length of the third side, so we have

`14+97>x\\\\\Rightarrow 111>x\\\\\Rightarrow x<111~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

`14+x>97\\\\\Rightarrow x>97-14\\\\\Rightarrow x>83~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

and

`97+x>14\\\\\Rightarrow x>14-97\\\\\Rightarrow x>-85~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(iii)`

From inequalities (i), (Ii) and (iii), we arrive at

`83<x<111\\\\\Rightarrow x>83.`

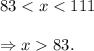
Thus, the length of the third side is greater than 83 mm.