Okay, here we have this:
We need to find the approximate distance between the two planes, let's do it:
Considering that we have right triangles we can use the pythagorean theorem.
For the measurement from the base of the tower to point S (x) we obtain:
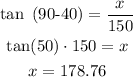
For the measurement from the base of the tower to point R (z) we obtain:
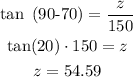
Now, to calculate the distance between the planes we are going to subtract the distance from each point to the base of the control tower:
Distance between the planes=178.76-54.59=124.17≈124.
Finally we obtain that the correct answer is the third option.