Question

An air traffic controller works at the top of a 150-foottower. From that point she measures the angle ofdepression to a plane at point S of 40°. Shemeasures the angle of depression to a second planeat point R of 70°.150feetSRWhich is closest to the distance between the twoplanes?44 ft0 73 ft

Answer 1

Okay, here we have this:

We need to find the approximate distance between the two planes, let's do it:

Considering that we have right triangles we can use the pythagorean theorem.

For the measurement from the base of the tower to point S (x) we obtain:

`\begin{gathered} \tan \text{ (90-}40)=(x)/(150) \\ \text{tan}(50)\cdot150=x \\ x=178.76 \end{gathered}`

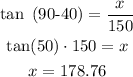
For the measurement from the base of the tower to point R (z) we obtain:

`\begin{gathered} \tan \text{ (90-7}0)=(z)/(150) \\ \tan (20)\cdot150=z \\ z=54.59 \end{gathered}`

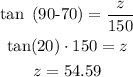
Now, to calculate the distance between the planes we are going to subtract the distance from each point to the base of the control tower:

Distance between the planes=178.76-54.59=124.17≈124.

Finally we obtain that the correct answer is the third option.