Answer:
The complex number in rectangular form is
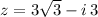 .
.
Explanation:
Let be a complex number in polar form, that is:
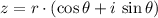 . The equivalent expression in rectangular form is defined by
. The equivalent expression in rectangular form is defined by
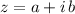 , where:
, where:
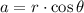 (1)
(1)
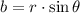 (2)
(2)
Where:
 - Magnitude.
- Magnitude.
 - Direction, measured in sexagesimal degrees.
- Direction, measured in sexagesimal degrees.
If we know that
 and
and
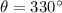 , then complex number in rectangular form is:
, then complex number in rectangular form is:

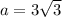
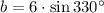
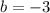
The complex number in rectangular form is
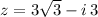 .
.