Answer:
x = 6
Explanation:
The given equation is

We write the equation in standard form of parabola
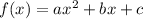 using FOIL
using FOIL

Now, we know that the axis of symmetry passes through the vertex. Hence, in order to find the vertex of the parabola, we find the x coordinate of the vertex.
x coordinate of the vertex is

Here, a = -1 b = 12

Therefore, the axis of symmetry is x = 6