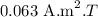Question

A rectangular loop of wire with a cross-sectional area of 0.234 m2 carries a current of 0.622 A. The loop is free to rotate about an axis that is perpendicular to a uniform magnetic field strength of 0.561 T. The plane of the loop is initially at an angle of 51.029o to the direction of the magnetic field. What is the magnitude of the torque on the loop ?

Answer 1

Given:

The area of the rectangular loop is,

`A=0.234\text{ m}^2`

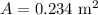
The current in the loop is,

`I=0.622\text{ A}`

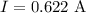
The strength of the magnetic field is,

`B=0.561\text{ T}`

The angle of the loop with the magnetic field is,

`\theta=51.029\degree`

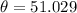
To find:

The magnitude of the torque on the loop

Step-by-step explanation:

The torque on a current-carrying loop is,

`\tau=IABsin\theta`

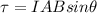
Substituting the values we get,

`\begin{gathered} \tau=0.622*0.234*0.561* sin51.029\degree \\ =0.063\text{ A.m}^2.T \end{gathered}`

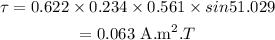
Hence, the torque is,

`\begin{equation*} 0.063\text{ A.m}^2.T \end{equation*}`