Answer:
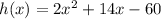
Explanation:
This question can be solved by two methods
Method 1: Substitute x=3 and x=-10 in all the equations and determine which equals to zero (ie., check h(3)=0 and h(-10)=0 for all the equations)
Equation 1
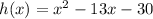
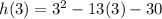
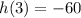
As h(3)≠0, Equation 1 is discounted
Equation 2
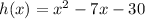

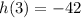
As h(3)≠0, Equation 2 is discounted
Equation 3
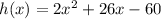
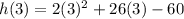
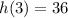
As h(3)≠0, Equation 3 is discounted
Equation 4
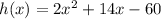
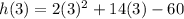
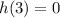
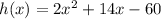
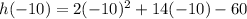
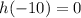
As h(3)=0 and h(-10)=0, Equation 4 represents h(x)
Method 2: Solve to find the roots of each equation where h(x)=0 using the quadratic formula. Roots should be x=3,x=-10
The quadratic formula is:
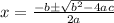
where a, b and c are as below
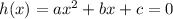
Equation 1
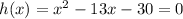
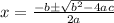

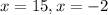
As roots are not x=3 and x=-10, Equation 1 is discounted
Equation 2
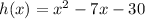
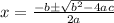
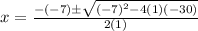
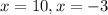
As roots are not x=3 and x=-10, Equation 2 is discounted
Equation 3
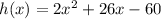
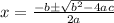
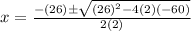
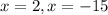
As roots are not x=3 and x=-10, Equation 3 is discounted
Equation 4
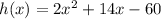
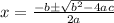
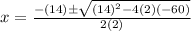
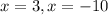
As roots are x=3 and x=-10, Equation 4 represents h(x)