18.9669 years
Step-by-step explanation:
principal = $1600
future value = $7600
rate = 8.3% = 0.083
n = number of times compounded = quarterly
n = 4
time = ?
To determine the time it will take, we will apply the compound interest formula:
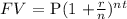
substitute the values into the formula:


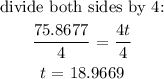
It will take 18.9669 years (4 decimal place)