Question

Hello, I am unsure how to get to the answer, can you include a sign chart as well for the second derivative thank you.

Answer 1

We want to find the intervals of concavity of the function;

`y=-x^4+8x^2-4`

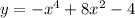
We start by taking the second derivatives;

`\begin{gathered} y^(\prime)=-4x^3+16x \\ y^(\prime)^(\prime)=-12x^2+16 \end{gathered}`

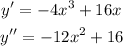
When a function is concave up, the second derivative is positive, thus; we seek the intervals where;

`\begin{gathered} -12x^2+16>0 \\ -12x^2>-16 \\ x^2<(16)/(12) \\ x^2<(4)/(3) \\ x<\pm\sqrt{(4)/(3)} \end{gathered}`

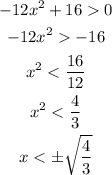
Let's find the points of inflection, this is where the second derivative is zero;

`\begin{gathered} -12x^2+16=0 \\ -12x^2=-16 \\ x^2=(16)/(12)=(4)/(3) \\ x=\pm(4)/(3) \end{gathered}`

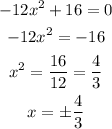
The y values will be;

`\begin{gathered} -((4)/(3))^4+8((4)/(3))^2-4=(44)/(9) \\ -(-(4)/(3))^4+8(-(4)/(3))^2-4=(44)/(9) \end{gathered}`

Thus, the answers are;

`\begin{gathered} Concave\text{ }up:(-\sqrt{(4)/(3)},\sqrt{(4)/(3)}) \\ Inflection\text{ }points:(-\sqrt{(4)/(3)},(44)/(9)),(\sqrt{(4)/(3)},(44)/(9)) \end{gathered}`

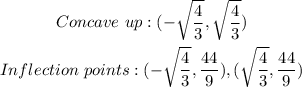
Thus the answer is option D;

This is a sign chart for the second derivative;