Let's use the variable x to represent the cost of one fishing reel and the variable y to represent the cost of one rod.
If 2 fishing reels and 5 rods cost $365, we have the equation:
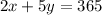
Then, if 4 reels and 2 rods cost $290, we have the second equation:
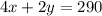
Let's divide the second equation by 2 and isolate the variable y:
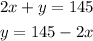
Then, let's use this value of y in the first equation:
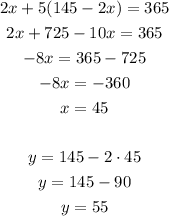
So the cost of one reel is $45 and the cost of one rod is $55.