Question

Determine whether the graphs of the given equations are parallel, perpendicular, or neither

y=x+11
y=-x+2

A.Parallel
B.Perpendicular
C.Neither

Answer 1

Perpendicular

Explanation:

Given are two equations as

`y=x+11\\y=-x+2`

We have to find whether these two are parallel or perpendicular or neither

For this first we have to find the slope of these two lines

I line slope = 1

II line slope =-1

Since slopes are not equal, the lines are not parallel.

Let us check product of these slopes. IF product =-1 the lines are perpendicular

We find that product =
`1*-1=-1`

Hence two lines are perpendicular

Answer 2

Keywords

parallel, perpendicular, graphing, linear equation, slope, lines

we know that

If two lines are perpendicular, then the product of their slope is equal to minus one

so

`m1*m2=-1`

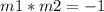
If two lines are parallel, then their slope are equal

`m1=m2`

In this problem we have

`y=x+11` --------> linear equation A

the slope is
`m1=1`

`y=-x+2` --------> linear equation B

the slope is
`m2=-1`

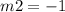
Find the product

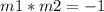`m1*m2=-1` ---------> the lines are perpendicular

therefore

the answer is the option B

Perpendicular

using a graphing tool

see the attached figure