State the given in the question.
It can be observed from the question that the following were given

State what we are supposed to find.
From the question, we are to find the probability of at least 10 workers.
In other to achieve this, the probability of at least 10 successes would be represented as below:
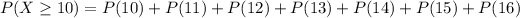
To find the individual probabilities for each success, X, we can either use a calculator's binomial probability distribution function (PDF), or we can use the binomial probability formula for each success, X. Then, find the sum of each of the individual probabilities.
For the question, we would solve for P(10) and P(11) using the binomial probability formula and use a calculator's binomial probability distribution function (PDF)
Let us find P(10) as shown below:
Please note that the binomial probability formula is given below:
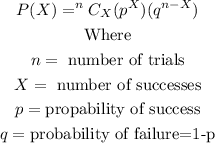
Therefore P(10) would be as calculated below:

P(11) is as calculated below:

Using the binomial distribution calculator

We can now use the above calculations to find the probability that at least 10 workers are fully remote

Hence, the probability that at least 10 workers are fully remote is 0.366030117