Question

Calculate the moments Mx, My, and the center of mass (x bar, y bar) of a lamina with the given density p=5 and the shape:

Answer 1

M x = 1/2 p ∫ ( f ( x )² - g ( x )² ) d x
f ( x ) = √( 1 - x²), g ( x ) = - 2

`M x = 1/2 * 5 \int\limits^1_(-1) (- x^(2) -3)\, dx= \\ =-5/2 * [ x^(3)/3 + 3 x]^1 _(-1) = \\ =-5/2 * (1/3+3+1/3+3)=`
= - 50/3
My = p ∫ x * ( f ( x ) ) dx
My = p ∫ x ( √(1+x²)) dx
Substitution: 1 - x² = u, x dx = - du/2

`M y = 5 * \int\limits^0_0 { √(u) } \, du = 0`
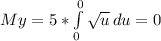M x = - 50/3, M y = 0

`M = 5 * \int\limits^1_(-1) { (\sqrt{1+ x^(2) }+2)} \, dx = \\ =5* [1/2 \sqrt{1+ x^(2) } *x + 2 x + 1/2 *sinh ^(-1) x]^1_(-1)`
M ≈ 5 * 6.3 ≈ 31.2
x = M y / M = 0 / 31.5 = 0
y = M x / M = -50/3 : 31.5 ≈ - 0.529
The center of mass is ( 0, -0.529 )